|
Accurate Normal Distribution for the HP67/97
|
|
06-26-2016, 09:34 PM
(This post was last modified: 04-22-2018 12:19 PM by Dieter.)
Post: #1
|
|||
|
|||
|
Accurate Normal Distribution for the HP67/97
Normal distribution for the HP67/97
This program for the HP67 and 97 evaluates various functions of the Standard Normal distribution:
Method and accuracy The Normal CDF is evaluated by two different methods. For 0 ≤ z ≤ 5 the upper-tail integral Q(z) is approximated by a (Near-)Minimax rational approximation: \(\large Q(z) \approx e^{-\frac{z^2}{2}} \cdot \frac{1+a_1z+a_2z^2+a_3z^3+a_4z^4}{2+b_1z+b_2z^2+b_3z^3+b_4z^4+b_5z^5}\) Using 10-digit coefficients the values are \(\begin{array}{ll} a_1=0,7981006015 & b_1=3,191970353\\ a_2=0,3111510842 & b_2=2,169125520\\ a_3=0,06328636234 & b_3=0,7932255604\\ a_4=0,005716530175 & b_4=0,1587036976\\ & b_5=0,01432712100 \end{array} \) If evaluated with sufficient precision, the relative error over the given domain is less than 2,6 E–10. With a few more digits the error can be reduced to approx. 2,41 E–10. For z > 5 the well known continued fraction expansion is applied, here with 8 terms: \(\large Q(z) \approx \frac{1}{\sqrt{2 \pi}} \cdot e^{-\frac{z^2}{2}} \cdot \cfrac{1}{z+\cfrac{1}{z+\cfrac{2}{z+\cfrac{3}{z+\dotsb}}}}\) The expression is calculated from right to left, starting not with 8/z but 8/(z+1,38) which significantly improves the resulting accuracy for smaller z. This way the relative error for z > 5 stays below 1 E-10 – provided the calculation is performed with sufficient precision. Due to the HP67/97's limitation to 10 significant digits and some numeric pitfalls the actual results on the HP67/97 will be less accurate. Since it is virtually impossible to verify the results over the complete domain I can only say that according to my results usually 9 significant digits (±1 unit) are achieved. See below for two exceptions. If you find substantially larger errors, please report here. The algorithm for the inverse (quantile function) first calculates a rough estimate by means of a simple rational approximation with an error of about ±0,002. The error of this first approximation is taylored for the following correction step that provides the final result. This is a very effective third order extrapolation due to Abramovitz & Stegun (1972) p. 954. With sufficient precision this method is good for about 11 significant digits over the calculator's complete working range down to 1 E–99. Again, the actual accuracy on the 67/97 is less and may drop to about 9 digits. But there is an exception: due to digit cancellation results very close to zero carry less significant digits, e.g. the quantile for a probability of 0,50003 is calculated as 7,5199 E–5. In such cases usually the remaining digits are fine, maybe within ±1 unit tolerance. So the result in FIX DSP 9 (0,000075199) should be OK. A similar limitation applies to the two-sided CDF for arguments very close to zero. Here you should not expect more than what you see in FIX DSP 9 mode (±1 digit). Evaluating the PDF seems trivial, but accuracy may degrade significantly for large arguments of the exponential function. For example e-1000/7 = 9,076766360 E-63, but the 67/97 returns 9,076765971 E-63. The error is caused by the fact that the fractional part of the argument carries only seven decimals which leads to an accuracy of merely seven significant digits. That's why the PDF is evaluated in a different way that requires three calls of ex, but achieves better accuracy. The program Here comes the listing. Code: 001 LBL BThe program expects the coefficients of the rational approximation in R1...R9. If it runs on a real (hardware) 67/97 this can be done by preparing a (single track) data card. The values for the constants have already been mentioned. Be sure to enter all ten digits: Code: R1 = 7,981006015 E-01The coefficients of the simple rational approximation for the quantile estimate are part of the program code. Of course they can just as well be stored in, say, the secondary registers S0...S3 and recalled from there. This will shorten the program and make the quantile calculation a tiny bit faster, but it requires a double-track data card. Usage Calculate the cumulative distribution function: z [A] The lower tail CDF P(z) is returned in X, the upper tail CDF Q(z) in Y. Calculate the symmetric two-sided cumulative distribution function: z [B] The two-sided CDF A(z) is returned in X, the complement 1–A(z) in Y. Calculate the quantile for a given lower-tail probability p: p [C] Calculate the quantile for a given two-sided symmetric probability p: p [D] Calculate the probability distribution function Z(z): z [E] Some examples In a soda water factory a machine fills bottles with an average volume of 503 ml. The content of the bottles varies slightly with a standard deviation of 5 ml. Determine the probability that a random soda bottle contains less than 490 ml. First calculate the Standard Normal variable z: Code: 490 [ENTER] 503 [-] 5 [÷] -2,600000000Now compute the lower tail CDF: Code: [A] 0,004661188So only 0,47% of all bottles will contain less than 490 ml while 99,53% exceed this volume. How much of the production will fall within ±10 ml around the mean volume? ±10 ml equals ±2 standard deviations. Code: 2 [B] 0,954499736In which interval around the mean will 98% of the production fall? So we are here looking for the two-sided quantile. Code: 0,98 [D] 2,326347874The tolerance interval is ±2,326 standard deviations. In absolute milliliters this is... Code: 5 [x] 11,63173937So 98% of the production is within 503 ± 11,63 ml. In the above example all digits displayed in FIX DSP 9 mode are exact. Here are some other results and their accuracy: Code: Q(0,01) = 0,4960106435 (-2 ULP)Cave: this does not mean that this accuracy level can be guaranteed. I have not found a case where the result was not within 1 unit in the 9th place, but please do your own tests. As usual, remarks, corrections and error reports are welcome. Finally, here are two (zipped) files for use with the Panamatic HP67 emulator. The first version implements the program listed above, the second version has the coefficients of the quantile estimate in registers S0...S3 and thus is a bit shorter. Dieter 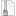 NormDist_67.zip (Size: 1.21 KB / Downloads: 28) NormDist_67.zip (Size: 1.21 KB / Downloads: 28)
|
|||
|
06-26-2016, 11:37 PM
Post: #2
|
|||
|
|||
|
RE: Accurate Normal Distribution for the HP67/97
This looks like a nice program, with very good documentation. I look forward to trying it on my RPN-67 simulator for iPad.
Regards, Bob |
|||
|
06-27-2016, 06:32 AM
Post: #3
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(06-26-2016 11:37 PM)bshoring Wrote: This looks like a nice program, with very good documentation. I look forward to trying it on my RPN-67 simulator for iPad. Thank you, Bob. I think a comprehensive documentation of the used methods is essential because this way the program may be translated for other calculators. Maybe I'll later post the 12-digit values of the coefficients for the newer models. Or even for the TI58/59. ;-) As a sidenote, I usually develop such rational approximations in Excel. But inverting a 9x9 matrix with sufficient accuracy simply was too much here. So the calculation was done on a WP34s which returned accurate results without any problem. Dieter |
|||
|
06-27-2016, 07:10 AM
Post: #4
|
|||
|
|||
| RE: Accurate Normal Distribution for the HP67/97 | |||
|
06-29-2016, 10:04 PM
(This post was last modified: 07-03-2016 02:42 PM by Dieter.)
Post: #5
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(06-27-2016 07:10 AM)Paul Dale Wrote: Yes, I really like the 34s for its sheer accuracy. Too bad the number of available registers does not allow anything larger than 9x9 matrices. Maybe I have to switch to Free42 for this. ;-) FWIW, after some more calculations (again on the 34s) I finally got something that should be close to the optimum under the given restrictions. Using sufficient precision, the relative error drops to ±1,7 E–10. To give you a visual impression, the error graph looks like this (click to view full size graphics). Blue: rational approximation, red: continued fraction with offset. The thin white lines define the 1,7 E–10 error interval. This result is achieved by changing the following values in the program listed in the initial post:
Due to the limited precision there is not much improvement in the 67/97 program, but maybe the values can be useful for an implementation on a different calculator. Dieter Edit: tweaked some coefficients in their last digit |
|||
|
06-30-2016, 01:57 AM
Post: #6
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(06-29-2016 10:04 PM)Dieter Wrote: Yes, I really like the 34s for its sheer accuracy. Too bad the number of available registers does not allow anything larger than 9x9 matrices. Maybe I have to switch to Free42 for this. ;-) Wouldn't 10x10 be possible? If not in the normal registers, in local ones. I thought we allowed local registers to be used for matrices. Pauli |
|||
|
06-30-2016, 12:11 PM
Post: #7
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(06-30-2016 01:57 AM)Paul Dale Wrote: Wouldn't 10x10 be possible? If not in the normal registers, in local ones. I thought we allowed local registers to be used for matrices. Could you give an example? This application requires solving a linear equation system. With 10 unknowns that's 120 registers (10x10 + 10 for the right hand side + 10 for the solution). Dieter |
|||
|
06-30-2016, 11:51 PM
(This post was last modified: 07-01-2016 12:00 AM by Paul Dale.)
Post: #8
|
|||
|
|||
|
RE: Accurate Normal Distribution for the HP67/97
Dieter,
You'll need to write a program that creates the locals and which finishes with STOP not RTN. E.g. to create a 10x10 identity matrix in local registers: Code: LBL ASwitch to run mode and XEQ A to run this. You can look at the first few using RCL . 00, RCL .01 etc. But to look at later values you need to use indirect addressing e.g. 167 RCL -> X returns 1 since it is a diagonal element. The first local register is accessed indirectly as register 112. Execute RTN in run mode to free the memory occupied by the locals. I'd probably put the two 10 long vectors into local registers instead of the large matrix. Although you can allocate 121 local registers, the matrix code doesn't allow a single matrix to have more than 100 elements. Pauli |
|||
|
07-01-2016, 09:22 PM
Post: #9
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(06-30-2016 11:51 PM)Paul Dale Wrote: I'd probably put the two 10 long vectors into local registers instead of the large matrix. I think that's what I'll try if I need to solve a 10x10 system. If I understand the idea behind local registers correctly they are discarded as soon as the program reaches a RTN (or an END). So some care is required. Dieter |
|||
|
03-22-2017, 10:13 PM
Post: #10
|
|||
|
|||
|
RE: Accurate Normal Distribution for the HP67/97
Users of RPN-67 and 97 simulators may download the program and data card here. (Scroll down to the Math section.)
|
|||
|
03-22-2017, 11:10 PM
(This post was last modified: 03-22-2017 11:47 PM by Dieter.)
Post: #11
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(03-22-2017 10:13 PM)Willy R. Kunz Wrote: Users of RPN-67 and 97 simulators may download the program and data card here. (Scroll down to the Math section.) I see that you included both sets of coefficients discussed earlier in this thread. Please note that also two other values that have to be changed! Switching to the optimized coefficient set also has to change the constants 5 and 1,38 that are hardcoded in the program, cf. line 27 resp. 33ff. Please read my comments on the three (!) required changes in post #5 of this thread. To be more clear: the program version you use will only work with the original, first set of coefficients. Using the alternate set with this program will result in reduced accuracy! I'd suggest you *only* use the modified coefficient set *and* change the mentioned two constants in the program to their modified values 4,679 resp. 1,422. This will require 226 program steps, so two steps have to be saved. This can be accomplished without significant disadvantages by rounding the constants to 4,68 and 1,42. (Of course you can also move these constants to register A and B on the data card and replace the respective program steps with RCL A resp. RCL B. ;-)) Dieter |
|||
|
03-23-2017, 04:43 PM
Post: #12
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(03-22-2017 11:10 PM)Dieter Wrote:(03-22-2017 10:13 PM)Willy R. Kunz Wrote: Users of RPN-67 and 97 simulators may download the program and data card here. (Scroll down to the Math section.) Sorry about overlooking those two bullet points. Late-night work... Quote:I'd suggest you *only* use the modified coefficient set *and* change the mentioned two constants in the program to their modified values 4,679 resp. 1,422. This will require 226 program steps, so two steps have to be saved. This can be accomplished without significant disadvantages by rounding the constants to 4,68 and 1,42. That's exactly what I did. Ready for download now. Of course, giving up vintage mode compatibility would allow adding bells and whistles, like full-precision constants and easy switching between the two models. Using RCL register arithmetic, single-line floating-point constants, INCR instead of "1 +" etc. would also make the program much shorter. And no data card required. Left as an exercise to the RPN-67 user... ;-) Willy |
|||
|
03-24-2017, 06:55 AM
Post: #13
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(03-23-2017 04:43 PM)Willy R. Kunz Wrote: That's exactly what I did. Ready for download now. Fine, thank you. (03-23-2017 04:43 PM)Willy R. Kunz Wrote: Of course, giving up vintage mode compatibility would allow adding bells and whistles, like full-precision constants and easy switching between the two models. Using RCL register arithmetic, single-line floating-point constants, INCR instead of "1 +" etc. would also make the program much shorter. And no data card required. I consider the Normal distribution CDF one of the most basic transcendental functions so that I wonder why it is not included as one of the "bells and whistles" of the extended version. ;-) BTW, what is the precision and working range of RPN-67? And does it use BCD or binary arithmetics? Dieter |
|||
|
04-20-2017, 02:13 PM
Post: #14
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(03-24-2017 06:55 AM)Dieter Wrote:(03-23-2017 04:43 PM)Willy R. Kunz Wrote: Of course, giving up vintage mode compatibility would allow adding bells and whistles, like full-precision constants and easy switching between the two models. Using RCL register arithmetic, single-line floating-point constants, INCR instead of "1 +" etc. would also make the program much shorter. And no data card required. I can't tell what version of RPN-67 you're using, but Normal distribution CDF has been part of RPN-67 since version 2.0 (Sep 2013). It's called NORM DIST. There's also Binomial Distribution, Negative Binomial Distribution, Bivariate Normal Distribution, and Poisson Distribution. However, I don't pretend RPN-67 is a statistical calculator, so some functions may be missing... ;-) Math uses standard double-precision binary libraries, although some additions/subtractions are done in BCD to avoid conversion errors. Willy |
|||
|
04-22-2018, 12:15 PM
(This post was last modified: 04-22-2018 12:35 PM by Dieter.)
Post: #15
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(04-22-2018 09:27 AM)Mike (Stgt) Wrote: After a while it displays 0.000025067 what is about 10 times more than your result. My assumption, there is a 0 missing in the entry, it should be 0.500001 Yes, of course there was a 0 missing in the input. Or one too much in the output. ;-) Very close to zero the quantile is approx. sqrt(2·pi) · (p–0,5). I have corrected the original post. BTW, with the adjusted coefficient set you should get 0,000025066 for p=0,50001, which is even more accurate. Dieter |
|||
|
12-02-2018, 07:44 PM
Post: #16
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(06-26-2016 09:34 PM)Dieter Wrote: The algorithm for the inverse (quantile function) first calculates a rough estimate by means of a simple rational approximation with an error of about ±0,002. The error of this first approximation is taylored for the following correction step that provides the final result. This is a very effective third order extrapolation due to Abramovitz & Stegun (1972) p. 954. What is the formula for the inverse cdf guess ? Is it this one ? https://www.johndcook.com/blog/normal_cdf_inverse/ I do not have access to the Abramovitz & Stegun book. Is third order correction faster than simple Newton's method ? Newton iteration: x = x - (CDF(x) - p) / PDF(x) |
|||
|
12-02-2018, 07:53 PM
Post: #17
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(12-02-2018 07:44 PM)Albert Chan Wrote: I do not have access to the Abramovitz & Stegun book. Everyone here should have a copy of this invaluable book. Copies available here for < $10.00, shipping included: https://www.abebooks.com/servlet/SearchR...l%20Tables --Bob Prosperi |
|||
|
12-02-2018, 10:08 PM
(This post was last modified: 12-02-2018 11:11 PM by Dieter.)
Post: #18
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(12-02-2018 07:44 PM)Albert Chan Wrote: What is the formula for the inverse cdf guess ? Is it this one ? No, that's the standard Hastings approximation which is also listed in the A&S book. But there are better ways. If you limit the domain for p to 1E–99 (underflow limit for most classic calculators) the error can be reduced by almost one magnitude, just by selecting different coefficients. The HP67/97 program above uses a much simpler custom approximation (line 113...152) which I designed myself. It is taylored to a certain error so that the following correction step yields about 11-digit accuracy for the Normal quantile if evaluated with sufficient precision. On the HP67/97 this means the result is about as good as it gets with 10 digit working precision. (12-02-2018 07:44 PM)Albert Chan Wrote: I do not have access to the Abramovitz & Stegun book. With internet access you have. The book is freely available online. Both as PDF as well as HTML-ized. However, many/most tables have been removed since today we have other means for calculating transcendental functions. ;-) (12-02-2018 07:44 PM)Albert Chan Wrote: Is third order correction faster than simple Newton's method ? Yes, significantly. After all, that's why I implemented it. ;-) Let t be the Newton correction term (p–Q(x))/Z(x), just as in your post (except the sign). Then the third-order correction uses expressions in t, t² and t³ to get a much better result: x := x + t + x/2 · t² + (2x²+1)/6 · t³ Newton's method uses only the first term t. Halley's method is comparable to the above series up to t². And with terms up to t³ even better results are obtained. The WP34s code for the Normal quantile also sets a rough estimate first (I don't remember the exact way, but I think I can look it up somewhere) and then merely two iterations are required to get a result with 30+ digit accuracy, only limited by the calculator's 34-digit working precision. Actually an computation with even higher precision would show that two approximations were even good for 40+ digits. So this really is a quite good extrapolation formula. Dieter |
|||
|
12-03-2018, 12:44 AM
Post: #19
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(12-02-2018 10:08 PM)Dieter Wrote: Let t be the Newton correction term (p–Q(x))/Z(x), just as in your post (except the sign). That is a cool formula ! I was expecting something much worse. To prove above correction work: f(x + h) = f(x) + f'(x) h + f''(x)/2 h² + f'''(x)/6 h³ + ... t = (f(x+h) - f(x)) / f'(x) = h + f''(x)/(2 f'(x)) h² + f'''(x)/(6 f'(x)) h³ + ... f'(x) = Z(x) = 1/√(2 pi) * exp(-x²/2), we get f''(x) = -x Z(x), and f'''(x) = (x² - 1) Z(x) t = h + (-x/2) h² + (x²-1)/6 h³ + ... (x/2) t² = (x/2) h² + (-3x²)/6 h³ + ... (2x²+1)/6 t³ = (2x²+1)/6 h³ + ... Sum it all, and ignore O(h4) terms, we get: x correction = h = t + x/2 · t² + (2x²+1)/6 · t³ |
|||
|
12-03-2018, 03:53 AM
Post: #20
|
|||
|
|||
RE: Accurate Normal Distribution for the HP67/97
(12-02-2018 07:44 PM)Albert Chan Wrote: I do not have access to the Abramovitz & Stegun book. You can download it for free using this link (470-page PDF, perfectly legal download): Handbook ... V. All My Articles & other Materials here: Valentin Albillo's HP Collection |
|||
|
« Next Oldest | Next Newest »
|
User(s) browsing this thread: 6 Guest(s)

 Search
Search Member List
Member List Calendar
Calendar Help
Help





